→ 문제 소개
“쓰레기 집수 풀"에 모인 쓰레기들을 비워내기 위해 Kruskal 알고리즘을 이용해 최소 비용으로 모든 노드를 연결하기

→ 기술 소개 및 문제 선정 이유
바다의 플라스틱(쓰레기)는 3분의 2이상이 강이나 하천에서부터 흘러온다.
이를 막기 위해서는 더이상 쓰레기가 흘러 바다로 오지 않도록 하천 쪽에 쓰레기 수거망을 설치해야한다.
42,000kg의 쓰레기를 모을 수 있는 쓰레기 배를 여러대 곳곳에 배치한다. 또 그 옆쪽으로는 거품 장벽을 배치해 쓰레기 조각이 기포에 걸려 표면으로 밀려나고, 그곳에서 물살에 의해 집수 풀(쓰레기 배)로 운반될 수 있도록 하는 기술이다.

이렇게 쓰레기 배(집수 풀)에 모인 쓰레기들은 모아서 다시 육지로 수거해 가야 한다.
이때 모든 노드를 최소 비용으로 거치며 모든 쓰레기 집수 풀의 쓰레기를 수거해갈 수 있도록 Kruskal 알고리즘을 사용했다.
원래는 다익스트라 알고리즘을 통해 해결하려 하였으나 다익스트라 알고리즘으로는 모든 노드를 통과할 수는 없기 때문에 Kruskal 알고리즘을 사용하게 되었다.
→ 사용할 언어
C++을 사용해 문제를 풀 예정이다.
→ 데이터 소개
쓰레기 소각장은 각 지역마다 있고 서울에도 양천구, 강남구, 노원구, 마포구에 있기 때문에 한 곳을 정해야 했다.
따라서 나는 노원구에 모일 쓰레기들만 고려할 예정이고, 노원구 근처의 쓰레기 집수 풀로부터 최단거리를 구했다.
데이터도 그 근처의 노원구, 성북구 등의 데이터만 사용하였다.
한 사람은 비교적 가까운 거리 안에서 사진을 찍었을 것이라고 가정하고 한 사람의 csv 파일의 경도 위도 값을 평균 내어 그 곳에 하나의 쓰레기 집수 풀을 설치한다고 생각하였다.
총 10명의 데이터를 사용했고, 그 값들을 평균 내어 위도 경도 값을 총 10개를 갖게 되었다.
이 열 곳에 각각 하나의 쓰레기 집수 풀이 있다고 가정했다.
따라서 열 곳에서의 최단 경로를 구하면 되는 것이다.
(1, 2, 4, 8, 11, 12, 14, 15, 16, 20 학생의 데이터를 사용하였다.)
→ 코드 설명
- 각 노드
각 노드는 임의로 0부터 9까지의 숫자를 매겨 0~9의 수를 가지도록 했다.
- 가중치 값
다익스트라 알고리즘을 사용하기 위해서는 가중치 값을 정해야 했다.
가중치 값은 두 지점을 이동하는데 걸리는 비용을 고려하기 위해 두 지점의 거리로 설정했다.
거리로 가중치를 설정하면 이동하는 데 걸리는 시간, 비용(기름값) 등을 모두 고려할 수 있기 때문이었다.
그냥 두 점 사이의 값을 계산하면 n.xx...형태의 매우 작은 값이 나왔기 때문에 결과값에 x10을 한 후 소수점은 제거해 주었다.
- 코드
1단계) 입력할 가중치를 txt 파일에 저장해 이 파일을 불러와 그래프에 가중치 정보를 저장하도록 한다.
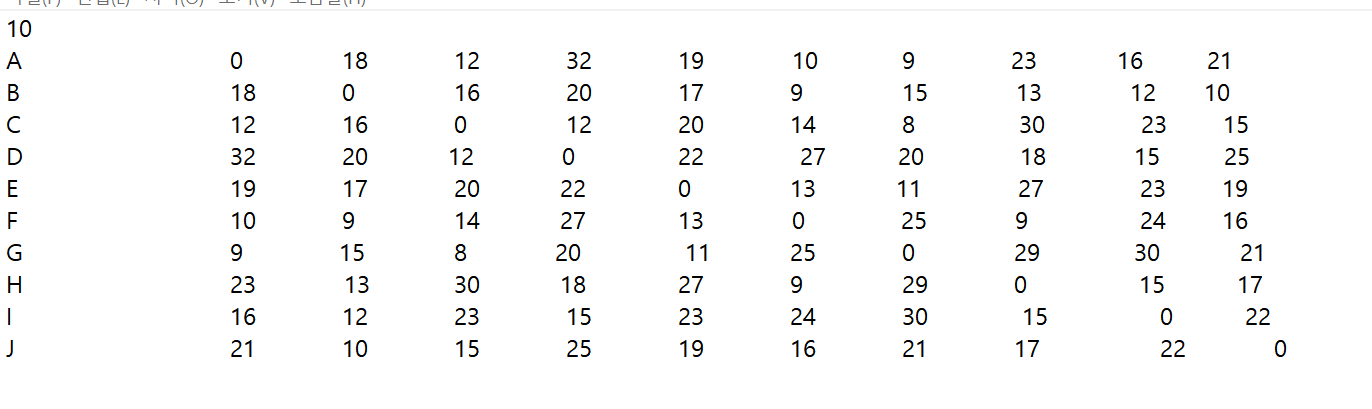
2단계) txt파일의 정보를 입력 받아 그래프 만들기
3단계) Kruskal 알고리즘을 실행하여 모든 노드 연결하기
-> 인접 행렬로 가중치 그래프를 만드는 class 를 작성한다.
-> 위의 그래프를 만들기 위해 노드, 가중치 값을 입력받는 class 를 작성한다.
-> Kruskal 알고리즘에서는 cycle이 있는지 검사해야 하므로
이를 위한 VertexSets class 를 작성한다.
-> Kruskal 알고리즘에서 힙 정렬 개념을 사용해 노드를 정렬하고
노드들을 최소 비용으로 연결하므로 이를 위한 HeapNode, MinHeap class 를 작성한다.
-> main 함수를 통해 파일을 읽게 한 후 그래프를 만들어
Kruskal 알고리즘을 실행하도록 한다.
#include <iostream>
#include <fstream>
using namespace std;
#define MAX_VTXS 100
#define INF 9999 // INF이면 간선없음
// 가중치 그래프를 표현하는 클래스
class AdjMatGraph {
protected:
int size;
char vertices[MAX_VTXS];
int adj[MAX_VTXS][MAX_VTXS];
public:
AdjMatGraph() { reset(); }
char getVertex(int i) { return vertices[i]; }
int getEdge(int i, int j) { return adj[i][j]; }
void setEdge(int i, int j, int val) { adj[i][j] = val; }
bool isEmpty() { return size == 0; }
bool isFull() { return size >= MAX_VTXS; }
void reset() {
size = 0;
for (int i = 0; i < MAX_VTXS; ++i)
for (int j = 0; j < MAX_VTXS; ++j)
setEdge(i, j, 0);
}
void insertVertex(char name) {
if (!isFull()) vertices[size++] = name;
else cout << "ERROR : 그래프 정점 개수 초과" << endl;
}
void insertEdge(int u, int v) {
setEdge(u, v, 1);
setEdge(v, u, 1);
}
void display() {
cout << size << endl;
for (int i = 0; i < size; ++i) {
cout << getVertex(i) << " ";
for (int j = 0; j < size; ++j)
cout << getEdge(i, j) << "\t";
cout << endl;
}
}
};
// 가중치 그래프를 표현하는 클래스
class WGraph : public AdjMatGraph {
public:
void insertEdge(int u, int v, int weight) {
if (weight > INF) weight = INF;
setEdge(u, v, weight);
}
bool hasEdge(int i, int j) { return (getEdge(i, j) < INF); }
void load(string filename) {
ifstream fp(filename);
if (fp.is_open()) {
int n, val;
fp >> n; // 정점의 전체 개수
for (int i = 0; i < n; i++) {
char str[80];
int val;
fp >> str; // 정점의 이름
insertVertex(str[0]); // 정점 삽입
for (int j = 0; j < n; j++) {
fp >> val; // 간선 정보
insertEdge(i, j, val); // 간선 삽입
}
}
}
else cout << "File can not be found !" << endl;
fp.close();
}
};
// 힙에 저장할 노드 클래스
#define MAX_ELEMENT 200
// 정점 집합 클래스 (Union-Find 연산)
class VertexSets {
int parent[MAX_VTXS]; // 부모 정점의 id
int nSets; // 집합의 개수
public:
VertexSets(int n) : nSets(n) {
for (int i = 0; i < nSets; i++)
parent[i] = -1; // 초기에 모든 정점이 고유의 집합에 속함
}
bool isRoot(int i) { return parent[i] < 0; }// -1이면 root
int findSet(int v) { // v가 속한 집합을 찾아 root 반환
while (!isRoot(v)) v = parent[v]; // v가 속한 집합의 루트를 찾음
return v;
}
void unionSets(int s1, int s2) { // 집합 s1을 집합 s2와 합침
parent[s1] = s2; // s1의 parent를 s2로 설정
nSets--; // 2개의 집합을 합쳐서 집합 개수는 1 감소
}
};
class HeapNode {
int key; // Key 값: 간선의 가중치
int v1; // 정점 1
int v2; // 정점 2
public:
HeapNode(int k = 0, int u = 0, int v = 0) : key(k), v1(u), v2(v) { }
void setKey(int k) { key = k; }
void setKey(int k, int u, int v) {
key = k; v1 = u; v2 = v;
}
int getKey() { return key; }
int getV1() { return v1; }
int getV2() { return v2; }
void display() {
cout << "\t" << "(" << v1 << "-" << v2 << ") -- " << key << endl;
}
};
class MinHeap {
HeapNode node[MAX_ELEMENT];
int size;
public:
MinHeap() : size(0) { }
bool isEmpty() { return size == 0; }
bool isFull() { return size == MAX_ELEMENT - 1; }
HeapNode& getParent(int i) { return node[i / 2]; }
HeapNode& getLeft(int i) { return node[i * 2]; }
HeapNode& getRight(int i) { return node[i * 2 + 1]; }
// 삽입 함수
void insert(int key, int u, int v) {
if (isFull()) return;
int i = ++size;
while (i != 1 && key < getParent(i).getKey()) {
node[i] = getParent(i);
i /= 2;
}
node[i].setKey(key, u, v);
}
// 삭제 함수
HeapNode remove() {
if (isEmpty()) return NULL;
HeapNode root = node[1];
HeapNode last = node[size--];
int parent = 1;
int child = 2;
while (child <= size) {
if (child < size
&& getLeft(parent).getKey() > getRight(parent).getKey())
child++;
if (last.getKey() <= node[child].getKey()) break;
node[parent] = node[child];
parent = child;
child *= 2;
}
node[parent] = last;
return root;
}
};
class WGraphMST : public WGraph {
public:
void Kruskal() { // kruskal의 최소 비용 신장 트리 프로그램
MinHeap heap;
// 1. 오름차순정렬 (heap sort)
for (int i = 0; i < size - 1; i++)
for (int j = i + 1; j < size; j++)
if (hasEdge(i, j))
heap.insert(getEdge(i, j), i, j); // 모든 간선 삽입
VertexSets set(size); // size개의 집합을 만듦
int edgeAccepted = 0; // 선택된 간선의 수
while (edgeAccepted < size - 1) { // 4.(n-1)개의 edge가 삽입될때까지
HeapNode e = heap.remove(); // 2.가장 작은 edge 선택
int uset = set.findSet(e.getV1()); // v1이 속한 집합의 루트 반환
int vset = set.findSet(e.getV2()); // v2가 속한 집합의 루트 반환
if (uset != vset) { // 3.사이클 생기지 않으면 MST삽입
cout << "간선 추가 : " << getVertex(e.getV1()) << " - " << getVertex(e.getV2()) << " (비용 : " << e.getKey() << ")" << endl;
set.unionSets(uset, vset); // 두개의 집합을 합함.
edgeAccepted++;
}
}
}
};
int main() {
WGraphMST g;
g.load("fin_graph.txt");
cout << "MST 크루스칼 알고리즘" << endl;
g.Kruskal();
return 0;
}
→ 코드 실행 결과
모든 노드를 최소 비용으로 연결할 수 있었다.

→ 유형 효과
최소한의, 필요한 거리만큼만 이동해 쓰레기를 수거함으로써 교통비, 이동 비용 등이 절감 된다.
Kruskal 알고리즘을 이용했기 때문에 최소 비용으로 움직일 수 있는 효율적인 방법이다.
→ 무형 효과
새로운 기술들을 도입하며 자라나는 미래의 개발자에게 창의력을 자극할 수 있다.
IT시대답게 IT기술로 환경 문제를 해결할 수 있다.
하천의 쓰레기들이 해양으로 흘러 가 해양쓰레기가 되어 더 큰 문제 발생하는 것을 막을 수 있다.
(여기서 더 큰 문제라 하면 해양쓰레기로 인한 자연 생물 파괴, 환경 오염 등을 해결하는 데 들어가는 비용을 아낄 수 있다는 의미)
(발표자료)