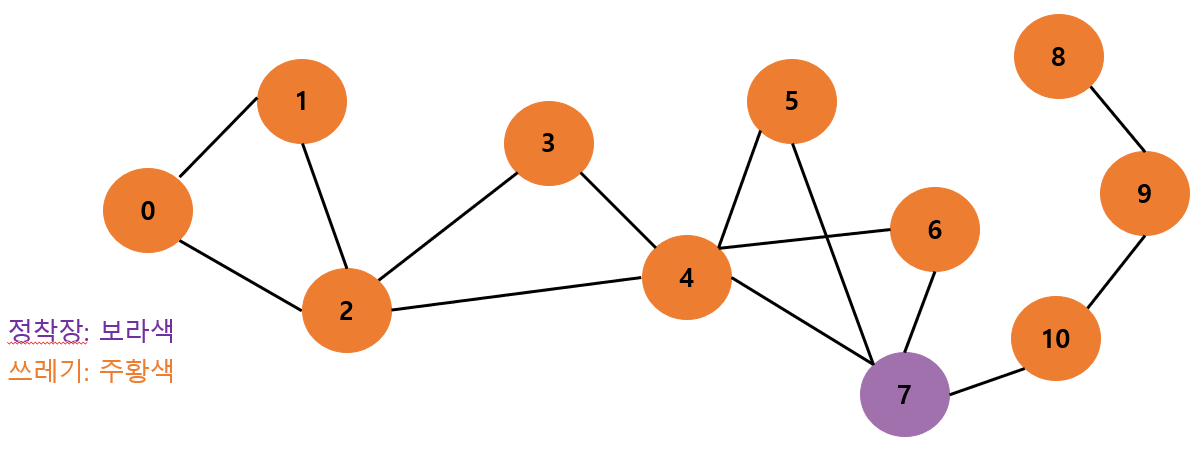
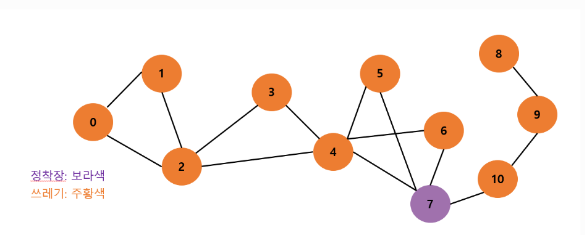
1. 그래프 예시를 직접 만들기
<문제>

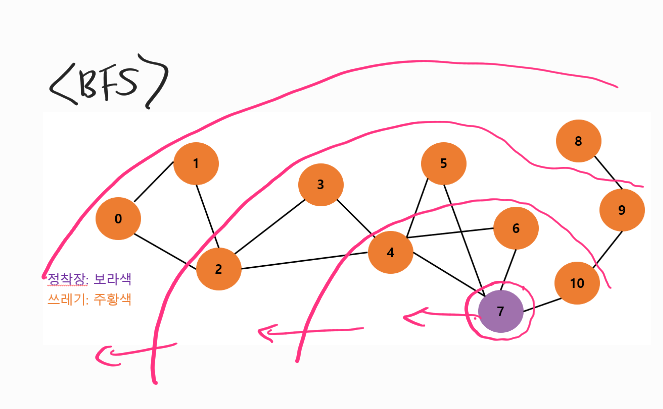
2. BFS와 DFS 알고리즘을 바탕으로 그래프 탐색 과정을 그리기
<BFS와 DFS의 차이점>
BFS는 넓이 우선 탐색으로, 한 노드에서 가장 인접한 노드를 탐색하고,
또 그 다음 노드들과 가장 인접한 노드들을 탐색해가는 알고리즘이며,
DFS는 깊이 우선 탐색으로, 미로 찾기처럼 한 노드를 정해
그 노드가 연결된 곳을 쭉 따라가 더이상 갈 곳이 없으면 다음 노드를 탐색하는 알고리즘이다.

자세한 탐색 과정은 아래 설명을 통해 확인해보겠다.
<BFS 알고리즘을 통한 그래프 탐색 과정>
1) 시작은 7부터 시작한다. 7을 큐에 넣는다.
2) 큐에 있는 숫자를 꺼내며 탐색을 시작한다.
- 7과 인접한 4, 5, 6, 10노드를 큐에 넣는다.
7은 방문했음으로 표시하고 큐에서 빼낸다.
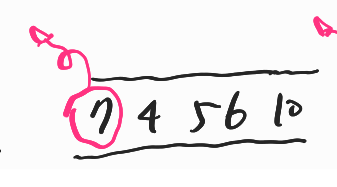
- 큐에 들어있는 4 노드에 대하여 탐색한다.
4와 인접한 2, 3노드를 큐에 넣는다.
4는 방문했음으로 표시하고 큐에서 빼낸다.
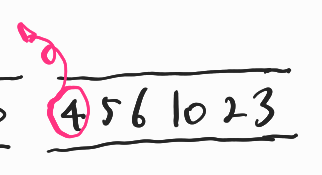
- 큐에 들어있는 5 노드에 대하여 탐색한다.
5와 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
5는 방문했음으로 표시하고 큐에서 빼낸다.

- 큐에 들어있는 6 노드에 대하여 탐색한다.
6과 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
6은 방문했음으로 표시하고 큐에서 빼낸다.
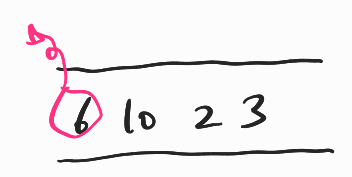
- 큐에 들어있는 10 노드에 대하여 탐색한다.
10과 인접한 노드는 9가 있으므로 큐에 넣어준다.
10은 방문했음으로 표시하고 큐에서 빼낸다.
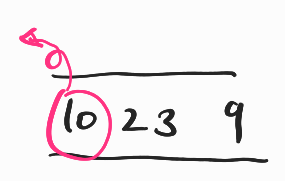
- 큐에 들어있는 2노드에 대하여 탐색한다.
2와 인접한 노드는 0, 1이 있으므로 큐에 넣어준다.
2는 방문했음으로 표시하고 큐에서 빼낸다.

- 큐에 들어있는 3 노드에 대하여 탐색한다.
3과 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
3은 방문했음으로 표시하고 큐에서 빼낸다.

- 큐에 들어있는 9 노드에 대하여 탐색한다.
9와 인접한 노드는 8이 있으므로 큐에 넣어준다.
9는 방문했음으로 표시하고 큐에서 빼낸다.
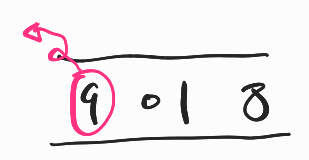
- 큐에 들어있는 0 노드에 대하여 탐색한다.
0과 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
0은 방문했음으로 표시하고 큐에서 빼낸다.

- 큐에 들어있는 1 노드에 대하여 탐색한다.
1과 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
1은 방문했음으로 표시하고 큐에서 빼낸다.
- 큐에 들어있는 8 노드에 대하여 탐색한다.
8과 더이상 인접한 노드는 없으므로 다음으로 넘어간다.
8은 방문했음으로 표시하고 큐에서 빼낸다.

8까지 빼내주면 순차적으로 모든 노드에 대해 BFS 탐색을 완료한 것이 된다.
<DFS 알고리즘을 통한 그래프 탐색 과정>
DFS 탐색 과정은 NULL이 나올 때까지 한 경로의 끝을 보는 탐색 방법이다.
7부터 최단거리를 탐색한다.
7 → 4 → 2 → 0 → 1 → NULL
다 탐색했으므로 뒤로 돌아간다.
7 → 4 → 2 → 0 (1에서 더 탐색할 곳 없음, 1삭제)
7 → 4 → 2 (0에서 더 탐색할 곳 없음, 0삭제)
2에서 더 갈 곳이 있으므로 2부터 다시 탐색한다.
7 → 4 → 2 → 3 → NULL
7 → 4 → 2 → 3 → 4 → NULL
7 → 4 → 2 → 3 → 4 → 5 → NULL
더이상 갈 곳이 없으므로 거꾸로 돌아간다.
7 → 4 → 2 → 3 → 4 → 5 → NULL
7 → 4 → 2 → 3 → 4
4에서 다시 갈 곳이 있으므로 탐색한다.
7 → 4 → 2 → 3 → 4 → 6 → NULL
6에서 더이상 갈 곳이 없으므로 되돌아간다.
7 → 4 → 2 → 3 → 4 → 6 → NULL
7 → 4 → 2 → 3 → 4 → NULL
7 → 4 → 2 → 3 → NULL
7 → 4 → 2 → NULL
7 → 4 → NULL
7 →
7부터 다시 안 가본 곳 탐색한다.
7 → 10
7 → 10 → 9
7 → 10 → 9 → 8
더이상 갈 곳이 없으니 되돌아 간다.
7 → 10 → 9 → 8 → NULL
7 → 10 → 9
7 → 10
7 →
모든 노드를 가봤으므로 탐색을 종료한다.
이와 같이 한 경로의 끝까지 탐색하여 최단거리를 구해 나간다.
3. BFS와 DFS 코드를 작성하기
<BFS 함수와 DFS 함수를 작성한 코드>
1) class CGraph에서 사용할 "벡터, 배열, 생성자, 인접 간선을 연결하는 함수,
BFS 함수, DFS 함수" 등을 선언하고 생성.
2) main 함수를 통해 인접한 간선들을 연결하고 함수를 실행.
→ 인접한 간선들을 setUndirectEdges() 함수를 통해 연결
→ 최단거리를 구할 시작점(쓰레기의 위치노드)인 n을 입력받음
→ BFS(), DFS() 함수를 실행해 최단거리 찾음
→ for문을 통해 결과 벡터에 저장한 값들을 순서대로 출력
#include <iostream>
#include <queue>
#include <list>
#include <vector>
using namespace std;
vector<int> result_bfs;
vector<int> result_dfs;
class CGraph {
private:
int n_vertices;
bool* visited;
vector<int> dist;
vector<list<int>> adj;
public:
CGraph(int _n_vertices) {
this->n_vertices = _n_vertices;
visited = new bool[_n_vertices];
for (int i = 0; i < _n_vertices; ++i) {
visited[i] = false;
}
dist.resize(_n_vertices);
adj.resize(_n_vertices);
}
~CGraph() {
delete visited;
}
void setUndirectEdges(int _s, int _d) {
adj[_s].push_back(_d);
adj[_d].push_back(_s);
}
void setDirectEdges(int _s, int _d) {
adj[_s].push_back(_d);
}
void BFS(int _s) {
visited[_s] = true;
queue<int> Q;
Q.push(_s);
while (!Q.empty()) {
_s = Q.front();
Q.pop();
result_bfs.push_back(_s);
list<int>::iterator iter;
for (iter = adj[_s].begin(); iter != adj[_s].end(); ++iter) {
if (!visited[*iter]) {
visited[*iter] = true;
Q.push(*iter);
dist[*iter] = dist[_s] + 1;
}
}
}
}
void DFS(int _s) {
visited[_s] = true;
result_dfs.push_back(_s);
list<int>::iterator iter;
for (iter = adj[_s].begin(); iter != adj[_s].end(); ++iter) {
if (!visited[*iter]) {
DFS(*iter);
}
}
}
};
int main() {
CGraph OGraph(11);
OGraph.setUndirectEdges(0, 1);
OGraph.setUndirectEdges(0, 2);
OGraph.setUndirectEdges(1, 2);
OGraph.setUndirectEdges(2, 3);
OGraph.setUndirectEdges(2, 4);
OGraph.setUndirectEdges(3, 4);
OGraph.setUndirectEdges(4, 5);
OGraph.setUndirectEdges(4, 6);
OGraph.setUndirectEdges(4, 7);
OGraph.setUndirectEdges(5, 7);
OGraph.setUndirectEdges(6, 7);
OGraph.setUndirectEdges(7, 10);
OGraph.setUndirectEdges(8, 9);
OGraph.setUndirectEdges(9, 10);
int n;
cout << "쓰레기의 위치를 입력하세요(0-10): ";
cin >> n;
OGraph.BFS(n);
OGraph.DFS(n); // 알고리즘을 실행
// 탐색하며 result 벡터에 넣어둔 값들을 하나씩 출력
cout << "BFS를 통한 최단거리: ";
for (int i = 0; i < result_dfs.size(); i++) {
cout << result_dfs[i] << " ";
}
cout << '\n';
cout << "DFS를 통한 최단거리: ";
for (int i = 0; i < result_dfs.size(); i++) {
cout << result_bfs[i] << " ";
}
return 0;
}
4. BFS 관련 문제를 풀어 보기
<백준 1260번: DFS와 BFS>
(1) 필요한 벡터, 배열 등을 선언한다.
→ 정점을 저장할 벡터, 방분 여부를 저장할 배열, BFS를 위한 벡터, DFS를 위한 벡터를 선언
(2) BFS 함수를 선언한다.
→ BFS 함수는 큐를 사용하여 구현함
→ 먼저 사용할 큐를 생성해줌
→ 시작점으로 입력받은 정점을 큐에 넣은 후 해당 노드를 방문했다고 바꿔줌
→ while문을 통해 큐 안에 들어있는 정점과 연결된(인접한) 정점들을 탐색하며
방문을 안한 노드라면 방문했다고 바꿔주고 큐에 넣음
(3) DFS 함수를 선언한다.
→ DFS 함수는 재귀함수를 통해 구현함
→ 시작점으로 입력받은 정점을 결과 벡터에 넣은 후 해당 노드를 방문했다고 바꿔줌
→ for문을 통해 인접한 정점들 중 방문하지 않은 곳일 때만 탐색하도록 DFS()함수를 다시 불러냄
(4) main 함수를 통해 원하는 실행을 하도록 한다.
→ 정점 개수와 값을 입력받아 벡터에 저장함
→ sort() 함수를 통해 낮은 숫자부터 탐색함
→ bfs함수와 dfs 함수를 실행한 후 결과 벡터에 들어있는 값을 하나씩 출력함
#include <iostream>
#include <vector>
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
vector<int> vec[10002];
vector<int> result_bfs;
vector<int> result_dfs;
bool visit[1002];
void bfs(int temp){
queue<int> q;
q.push(temp);
visit[temp] = true;
while(!q.empty()){
int x = q.front();
q.pop();
result_bfs.push_back(x);
for (int i = 0; i < vec[x].size(); i++){
if(!visit[vec[x][i]]){ //방문하지 않은 곳만 탐색
q.push(vec[x][i]);
visit[vec[x][i]] = true;
}
}
}
}
void dfs(int x){
visit[x] = true;
result_dfs.push_back(x);
for (int i = 0; i < vec[x].size(); i++){
if(!visit[vec[x][i]]){ //방문하지 않은 곳만 탐색
dfs(vec[x][i]);
}
}
}
int main(){
int n, m, v, a, b;
cin >> n >> m >> v;
for (int i = 1; i <= m;i++){
cin >> a >> b;
vec[a].push_back(b); //양방향 간선처리
vec[b].push_back(a); //양방향 간선처리
}
for (int i = 1; i <= n;i++){
sort(vec[i].begin(), vec[i].end()); // 낮은 숫자부터 탐색.
}
bfs(v);
memset(visit, false, sizeof(visit));
dfs(v);
for (int i = 0; i < result_dfs.size() ;i++){
cout << result_dfs[i] << " ";
}
cout << '\n';
for (int i = 0; i < result_bfs.size() ;i++){
cout << result_bfs[i] << " ";
}
return 0;
}