앞에서 내가 만들었던 데이터를 여기에도 적용해 실행해보겠다. (연봉 액수에 따른 행복도 예측)
<경사하강법 실습>
앞의 장에서 사용했던 최소 제곱법이 아닌 평균 제곱 오차와 경사하강법으로 같은 문제를 해결할 수 있음을 알게 되었다.
1. 데이터 리스트 부분만 변경해 데이터를 그래프로 나타냈다.

2. 학습률을 0.006으로 수정하고 코드를 돌려보니 3장에서 선형회귀 코드로 출력한 결과와 비슷한 기울기와 y절편 값을 구할 수 있었다.

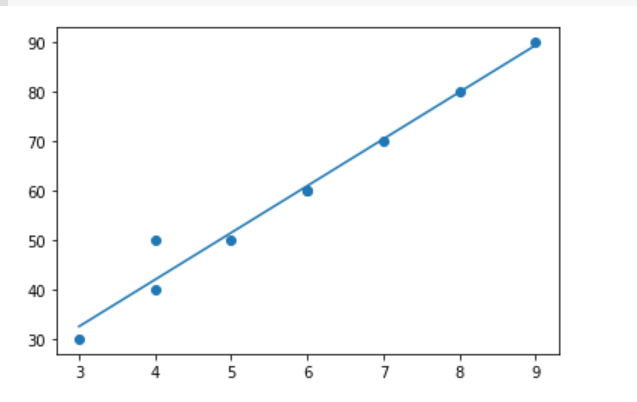
3. 앞에서 구한 기울기와 절편으로 그래프를 다시 그려보았다.
<다중 선형 회귀 실습>
다중 선형 회귀는 그냥 선형 회귀와 달리 독립변수 x가 여러 개이기 때문에 여러가지가 달라진다.
1. 1차원 예측 직선 -> 3차원 예측평면 으로 바뀜
(3차원 예측 평면을 그릴 수 있는 코드가 더 필요)
2. 변수를 여러 개 고려하게 되기 때문에 더 정밀하고 정확한 예측이 가능해진다.
다중 선형 회귀 예제를 활용하기 위해선 추가적인 데이터가 더 필요했다.
추가적인 독립변수 x2는 '언제든 가볍게 만날 수 있는 친구의 수'로 결정했다.
사용할 데이터 :
연봉 액수 (단위: 천 만원) | 3 | 4 | 4 | 5 | 6 | 6 | 7 | 8 | 9 |
-----------------------------------------------------------------------------------------------------------------
친구의 수 (단위: 명) | 3 | 5 | 4 | 5 | 6 | 6 | 7 | 8 | 9 |
-----------------------------------------------------------------------------------------------------------------
행복도 | 30 | 50 | 40 | 50 | 60 | 60 | 70 | 80 | 90 |
1. 데이터 부분만 변경하여 실행해 그래프를 출력해보았다.

2. 학습률만 변경해 다음과 같이 기울기1,2와 y 절편 값을 구했다.

3. 마지막으로 3차원 예측 평면 (3D)을 출력했다.

'딥러닝 실습' 카테고리의 다른 글
| [모두의 딥러닝] 5장 예제 실습, 활용 (참 거짓 판단 장치: 로지스틱 회귀) (0) | 2022.01.17 |
|---|---|
| [모두의 딥러닝] 3장 예제 : 선형 회귀 실습 (0) | 2022.01.12 |
| [모두의 딥러닝] 1장 예제 : 폐암 수술 환자의 생존율 예측하기 실습 (0) | 2022.01.12 |